问题
多选题
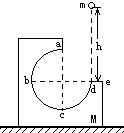
如图,M为固定在桌面上的L形木块,abcd为3/4圆周的光滑轨道,a为轨道的最高点,de面水平且有一定长度.今将质量为m的小球在d点的正上方高h处释放,让其自由下落到d处切入轨道运动,则( )
A.在h一定的条件下,释放后小球的运动情况与小球的质量有关
B.只要改变h的大小,就能使小球通过a点之后,既可能落回轨道之内,又可能落到de面上
C.无论怎样改变h的大小,都不可能使小球通过a点之后,又落回轨道之内
D.要使小球飞出de面之外(即e的右面)是可能的
答案
A、释放后小球只受重力,根据动能定理得:
mgh=
mv2,1 2
v=2gh
所以在h一定的条件下,释放后小球的运动情况与小球的质量无关,故A错误;
B、C、D、当小球运动到a点时,临界条件是木块对小球的支持力为零,
则mg=m
,即v=v2 R
,所以要使小球通过a点,小球在a点速度va≥gR
.gR
小球通过a点后做平抛运动,
竖直方向:R=
gt2 即t=1 2 2R g
∴水平方向:s=vat≥
R>R,即小球通过a点后,小球不能落回轨道内,2
由于de面长度不清楚,所以小球通过a点后,可能落到de面上,也有可能可能落到de面右侧之外.故B错误,C正确,D正确.
故选CD.
