问题
填空题
多项式x2+mx+5因式分解得（x+5）（x+n），则m= ，n= ．
答案
6，1
题目分析：将（x+5）（x+n）展开，得到，使得x2+（n+5）x+5n与x2+mx+5的系数对应相等即可：
∵（x+5）（x+n）=x2+（n+5）x+5n，∴x2+mx+5=x2+（n+5）x+5n。
∴
。
搜题请搜索小程序“爱下问搜题”
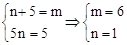多项式x2+mx+5因式分解得（x+5）（x+n），则m= ，n= ．
6，1
题目分析：将（x+5）（x+n）展开，得到，使得x2+（n+5）x+5n与x2+mx+5的系数对应相等即可：
∵（x+5）（x+n）=x2+（n+5）x+5n，∴x2+mx+5=x2+（n+5）x+5n。
∴。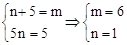