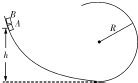
如图所示,在紧直面内有一个光滑弧形轨道,其末端切线水平,且与处于同一竖直面内光滑圆形轨道的最低端相切,并平滑连接.A、B两滑块(可视为质点)用轻细绳拴接在一起,在它们中间夹住一个被压缩的微小轻质弹簧.两滑块从弧形轨道上的某一高度南静止滑下,当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开,弹簧迅速将两滑块弹开,其中前面的滑块A沿圆形轨道运动.已知圆形轨道的半径R=0.50m,滑块A的质量mA=0.16 kg,滑块B的质量mB=0.04kg,两滑块开始下滑时距圆形轨道底端的高度,h=0.80m,重力加速度g取1 0m/s2,空气阻力可忽略不计.试求:
(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小;
(2)若滑块A在最低点被弹簧弹开时的速度大小为5.0m/s,求A滑到最高点时对轨道的压力大小.
(1)设A、B两滑块一起运动到圆形轨道最低点时速度的大小为v0,此过程机械能守恒,则有
(mA+mB)gh=
(mA+mB)1 2 v 20
解得 v0=4m/s
(2)设滑块A在最低点被弹簧弹开时的速度大小vA,到达最高点时速度大小为v,对于滑块从最低点到最高点的过程中,根据机械能守恒定律得
mA1 2
=mAg?2R+v 2A
mAv21 2
在最高点,F+mAg=mv2 R
联立解得,轨道对小球的弹力为F=0,
则根据牛顿第三定律得知,A滑到最高点时对轨道的压力大小为零.
答:
(1)A、B两滑块一起运动到圆形轨道最低点时速度的大小是4m/s;
(2)A滑到最高点时对轨道的压力大小是零.
