问题
问答题
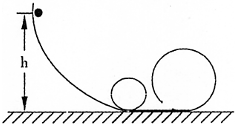
如图所示,一条圆弧轨道与大小不同的两个圆环轨道连接在一起,质量为m的小球从高为h处由静止开始滑下,在小环(底部稍错开一些)内侧运动一周后.刚好能通过大环的最高点.若大环的半径是小环半径的2倍,轨道表面光滑,不计空气阻力,重力加速度为g,求
(1)小环的半径r;
(2)小球通过小环的最高点时对小环的压力大小.
答案
(1)大环半径为2r,在大环最高点由牛顿第二定律得mg=mv 22 2r
小球从开始下滑到大环最高点过程机械能守恒 mgh=4mgr+
m1 2 v 22
由以上两式解得r=h 5
(2)小球从开始下滑到小环最高点过程机械能守恒.mgh=2gmr+
m1 2 v 21
在小环最高点时,由牛顿第二定律得 F+mg=mv 21 r
由以上两式解得F=5mg
由牛顿第三定律知球对小环压力大小为F'=5mg.
