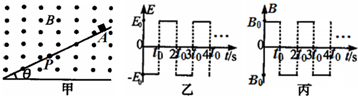
一倾角θ=30°的足够长的绝缘斜面，P点上方光滑，P点下方粗糙，

问题问答题

一倾角θ=30°的足够长的绝缘斜面，P点上方光滑，P点下方粗糙，处在一个交变的电磁场中，如图甲所示，电磁场的变化规律如图乙和丙所示，磁场方向以垂直纸面向外为正，而电场的方向以竖直向下为正，其中B0=

2πm

qt0

，E0=

，现有一带负电的小物块（可视为质点，其质量为m、带电量为q）从t=0时刻由静止开始从A点沿斜面下滑，在t=3t₀时刻刚好到达斜面上的P点，并且从t=5t₀时刻开始物块在以后的运动中速度大小保持不变．若已知斜面粗糙部分与物块间的动摩擦因素为μ=

，还测得在0～6t₀时间内物块在斜面上发生的总位移为4g

，求：

（1）小球在t₀时刻的速度；

（2）在整个运动过程中物块离开斜面的最大距离；

（3）物块在t=3t₀时刻到t=5t₀这段时间内因为摩擦而损失的机械能．（计算中取π²=10）

答案

（1）0～t₀内小物块匀加速下滑：

F_合=（mg+E₀q）sinθ=ma

得a=g

故v=at₀=gt₀

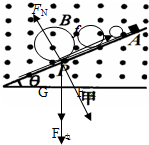
（2）运动轨迹如图，物体在5t₀之后匀速，速度达到最大，有：

F_N=B₀qv_m+（mg+Eq₀）cosθ

（mg+Eq₀）sinθ=μF_N

由以上两式得到：v_m=

gt0

在5t₀～6t₀时间内物块脱离斜面做匀速圆周运动：B₀qv_m=m

得到r=

mvm

B0q

π2

物块离开斜面的最大距离为△l=2r=

π2

（3）0～t₀内：x1=

2t₀～3t₀内：x2=

a(2t0)2-x1=

4t₀～5t₀内：x3=x-x1-x2=2g

P点速度为v=a•2t₀=2gt₀

根据动能定理得到：(mg+Eq0)x3sinθ-W=

得到摩擦损失的机械能为：W=1.6mg2

答：

（1）小球在t₀时刻的速度为gt₀；

（2）在整个运动过程中物块离开斜面的最大距离为

π2

；

（3）物块在t=3t₀时刻到t=5t₀这段时间内因为摩擦而损失的机械能为1.6mg2

．