问题
问答题
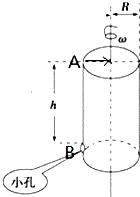
如图,横截面积半径为R的转筒,转筒顶端有一A点,其正下方有一小孔B,距顶端h=0.8m,开始时,转筒的轴线与A点、小孔B三者在同一竖直平面内.现使一小球自A点一速度v=4m/s朝转筒轴线水平抛出,同时转筒立刻以某一角速度匀速转动起来,小球未碰到筒.壁且正好从小孔B穿出,不计空气阻力,g取10m/s2,求:
(1)转筒半径R;
(2)转筒转动的最小角速度取ω;
(3)转筒转动的角速度能否为10πrad/s.
答案
(1)小球从A点开始做平抛运动,
设小球从A点到进入小孔的时间为t
竖直方向做自由落体运动,h=
gt2①1 2
水平方向做匀速直线运动,
则2R=vt ②
由①、②联立解得
R=0.8 m ③
故转筒半径R为0.8m.
(2)在小球到达小孔的时间t内,圆桶必须恰好转过半周的奇数倍,小球才能钻出小孔
则ωt=(2n+1)π(n=0,1,2…)
由①可得小球到达小孔的时间
t=0.4s
解得ω=(5n+2.5)πrad/s(n=0,1,2…)
所以转筒转动的最小角速度为2.5πrad/s
(3)因为5n+2.5(n=0,1,2…) 不可能取到10
所以ω=(5n+2.5)πrad/s(n=0,1,2…) 不可能等于10πrad/s.
答:(1)转筒半径R为0.8m;
(2)转筒转动的最小角速度为2.5πrad/s;
(3)转筒转动的角速度不能为10πrad/s.
