如图是检验某种防护罩承受冲击能力的装置，M为半径R=1.6m、固定

问题问答题

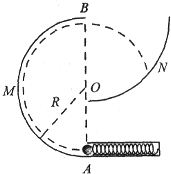
如图是检验某种防护罩承受冲击能力的装置，M为半径R=1.6m、固定于竖直平面内的光滑半圆弧轨道，A、B分别是轨道的最低点和最高点；N为防护罩，它是一个竖直固定的1/4圆弧，其半r=

m，圆心位于B点．在A放置水平向左的弹簧枪，可向M轨道发射速度不同的质量均为m=0.01kg的小钢珠，弹簧枪可将弹性势能完全转化为小钢珠的动能．假设某次发射的小钢珠沿轨道恰好能经过B点，水平飞出后落到N的某一点上，取g=10m/s²．求：

（1）钢珠在B点的速度；

（2）发射该钢珠前，弹簧的弹性势能Ep；

（3）钢珠从M圆弧轨道B点飞出至落到圆弧N上所用的时间．

答案

（1）在B处对小钢珠进行受力分析，钢珠沿轨道恰好能经过B点，由牛顿第二定律得

mg=

得：v_B=

=4m/s

（2）从发射钢珠到上升到B点过程，

由机械能守恒定律得

E_pN=△E_PG+△E_k=mg×2R+

得E_pN=0.4J

（3）钢珠做平抛运动，由平抛运动的规律得：

gt²

x=v_Bt

x²+h²=r²

联立解得t=0.4s

答：（1）钢珠在B点的速度是4m/s；

（2）发射该钢珠前，弹簧的弹性势能是0.4J；

（3）钢珠从M圆弧轨道B点飞出至落到圆弧N上所用的时间是0.4s．