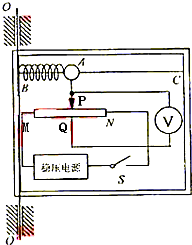
使用“弹簧式角速度测量仪”可以测量运动装置自转时角速度的大小,其结构示意图如图所示.将测量仪固定在待测装置上,当装置绕竖直固定轴OO′转动时,与轻弹簧相连的小球A可在光滑绝缘细杆BC上滑动,同时带动连接在A上的滑动变阻器的动触片P在与BC平行的电阻丝MN上滑动,使得电压表V的示数U0随装置转动的角速度ω发生变化,据此可测出待测装置的角速度ω的大小.
已知:小球A的质量为m;弹簧的原长为x0、劲度系数为k;电阻MN粗细均匀、长度为L、阻值为R;电压表V通过两根导线分别接在电阻丝MN的中点Q和动触片P上,电阻丝MN的两端接在电压为U的直流稳压电源上.闭合开关后S测量仪器即可工作.若不计导线和动触片P的电阻、以及导线对动触片P的影响,忽略动触片P和电阻MN之间的摩擦,且电压表视为理想电表.装置静止时,动触片P与Q(导线和电阻的连接点)重合.
(1)试推导:待测装置自转的角速度ω与电压表V的示数U0之间的关系式.
(2)用该测量仪能测量的自转角速度的最大值ωm是多少?
(1)设待测装置自转的角速度为ω时,弹簧伸长量为x,电压表V的示数为U0,小球A做圆周运动的半径为 r=x0+x,弹簧弹力为F.
根据牛顿第二定律,有 F=mω2r ①
由胡克定律 F=kx ②
电压表V的示数(即P、Q间的电压)为U0,设P、Q间的电阻值为Rx,有
=U0 U
=Rx R
③x L
①、②、③式联立,得ω=
④k m(1+
)x0U LU0
(2)用该测量仪测量某装置自转的角速度为最大值ωm时,有:
x=
L ⑤1 2
U0=
U ⑥1 2
代入④式,得 ωm=k m(1+
)2x0 L
答:(1)待测装置自转的角速度ω与电压表V的示数U0之间的关系式为
.k m(1+
)x0U LU0
(2)用该测量仪能测量的自转角速度的最大值ωm是
.k m(1+
)2x0 L
