如图所示,质量为m=0.10kg的小球和A、B两根细绳相连,两绳固定在细杆的A、B两点,其中A绳长LA=2.0m,当两绳都拉直时,A、B两绳和细杆的夹角θ1=37°,θ2=53°.求:(g=10m/s2,sin37°=0.6,cos37°=0.8,计算结果保留两位有效数字)
(1)当细杆转动的角速度ω在什么范围内,A、B两绳始终张紧?
(2)当ω=3rad/s时,A、B两绳的拉力分别为多大?
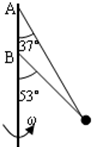
(1)当B绳恰好拉直,但TB=0时,细杆的转动角速度为ω1,
有:TAcos37°=mgTAsin370=m
LAsin370ω 21
解得:ω1=2.5rad/s
当A绳恰好拉直,但TA=0时,细杆的转动角速度为ω2,
有:TBcos530=mgTBsin530=m
LAsin370ω 22
解得:ω2=3.3rad/s
要使两绳都拉紧2.5 rad/s≤ω≤3.3rad/s
(2)当ω=3 rad/s时,两绳都拉紧.TAsin37°+TBsin53°=mω2LAsin37°
TAcos37°+TBcos53°=mg
TA=0.54N
TB=0.94N
答:(1)要使两绳都拉紧2.5 rad/s≤ω≤3.3rad/s.
(2)当ω=3rad/s时,A、B两绳的拉力分别为TA=0.54N,TB=0.94N.
