问题
多选题
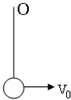
如图所示,一根长为L的轻绳的一端系一质量为m的小球,另一端固定在O点,当小球在最低点时突然获得一初速度V0,使小球能绕O点做圆周运动,小球能上升的最大高度hmax可能是( )
A.hmax>v 20 2g
B.hmax<v 20 2g
C.hmax=v 20 2g
D.hmax=2L
答案
(1)小球做圆周运动,恰好达到最高点时,
由牛顿第二定律得:m
=mg ①,v2 L
从最低点到最高点的过程中,由能量守恒定律得:
mv02=1 2
mv2+mg×2L ②,1 2
由①②得:小球做圆周运动,恰好通过最高点时,
mv02=5mgL,则当时,小球能做完整的圆周运动,
小球上升的最大高度hmax=2L,故D正确;
由mv02≥5mgL,得:L≤
,2L≤v 20 5g
<2 v 20 5g
,故B正确;v 20 2g
(2)当mv02<5mgL时,小球不能做完整的圆周运动,
上升的最大高度小于2L,从最低点到最高点的过程中,
由机械能守恒定律可得:
mv02=mghmax,1 2
则hmax=
,故C正确;v 20 2g
由(1)(2)的分析可知:hmax≤
,故A错误;v 20 2g
故选BCD.
