问题
多选题
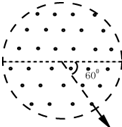
如图所示为圆柱形区域的横截面,在没有磁场的情况下,带电粒子(不计重力)以某一初速度沿截面直径方向入射,穿过此区域的时间为t,在该区域加沿轴线方向的匀强磁场,磁感应强度为B,带电粒子仍以同一初速度沿截面直径入射,粒子飞出此区域时,速度方向偏转60°角,如图所示,根据上述条件可求下列物理量中的( )
A.带电粒子的比荷
B.带电粒子在磁场中运动的周期
C.带电粒子在磁场中运动的半径
D.带电粒子的初速度
答案
无磁场时,带电粒子做匀速直线运动,设圆柱形区域磁场的半径为R0,则v=2
(1)R0 t
而有磁场时,带电粒子做匀速圆周运动,由半径公式可得:R=
(2)mv Bq
由几何关系得,圆磁场半径与圆轨道半径的关系:R=
R0 (3)3
由(1)(2)(3)联式可得:
=q m 2
Bt3
设粒子在磁场中的运动时间t0,
粒子飞出此区域时,速度方向偏转60°角,则由周期公式可得:t0=
=T 6
πt3 6
由于不知圆磁场的半径,因此带电粒子的运动半径也无法求出,以及初速度无法求.
故选:AB
