问题
问答题
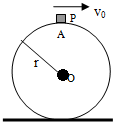
如图所示,横截面半径为r的圆柱体固定在水平地面上.一个质量为m的小滑块P从截面最高点A处以v0=
滑下.不计任何摩擦阻力.2rg 5
(1)试对小滑块P从离开A点至落地的运动过程做出定性分析;
(2)计算小滑块P离开圆柱面时的瞬时速率和落地时的瞬时速率.
下面是某同学的一种
(1)小滑块在A点即离开柱面做平抛运动,直至落地.
(2)a、滑块P离开圆柱面时的瞬时速率为v0=
.2rg 5
b、由:
mv02+mg2r=1 2
mvt2得:1 2
落地时的速率为vt=22rg 5
你认为该同学的解答是否正确?若正确,请说明理由.若不正确,请给出正确解答.
答案
(1)这位同学对过程的分析错误,物块先沿着圆柱面加速下滑,然后离开圆柱面做斜下抛运动,离开圆柱面时的速率不等于v0.
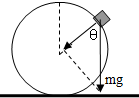
(2)a、设物块离开圆柱面时的速率为v,则有
mgcosθ=mv2 r
根据机械能守恒得:mgr(1-cosθ)=
mv2-1 2
mv021 2
解得:v=4rg 5
b、由:
mv02+mg2r=1 2
mvt2得:1 2
落地时的速率为vt=22rg 5
答:(1)这位同学对过程的分析错误,物块先沿着圆柱面加速下滑,然后离开圆柱面做斜下抛运动,离开圆柱面时的速率不等于v0.
(2)a、滑块P离开圆柱面时的瞬时速率为
.b、落地时的速率为4rg 5
.22rg 5
