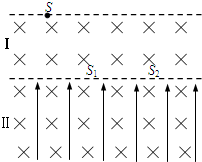
如图所示自上而下分为Ⅰ、Ⅱ二个区域,在Ⅰ、Ⅱ中分布有垂直纸面向里的匀强磁场,区域Ⅰ宽度为d,区域Ⅱ中还分布有沿纸面竖直向上的匀强电场.现有一质量为m,电量为q的尘粒,从区域Ⅰ上边缘的S处由静止开始运动,然后以与界面成α角的方向从S1处进入Ⅱ区域,尘粒在Ⅱ区域中刚好做匀速圆周运动,最后通过S2回到Ⅰ区域,已知S1到S2的距离为L,重力加速度为g.求:
(1)该尘粒在进入Ⅱ区域时的速率
(2)匀强电场的电场强度和匀强磁场的磁感应强度的大小
(3)欲使微粒能进入Ⅱ区域,区域Ⅰ宽度d应满足的条件.
(1)尘粒在磁场Ⅰ中运动时,根据动能定理,得
mgd=
mv2,得到v=1 2 2gd
(2)尘粒在Ⅱ区域中做匀速圆周运动,则有mg=qE
得到E=
,方向竖直向上,说明尘粒带正电.mg q
根据几何知识求出尘粒匀速圆周运动的半径R=L 2sinα
由牛顿第二定律,得qvB=m
,代入解得v2 R
B=2m
sinα2gd qL
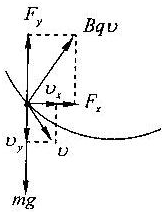
(3)尘粒在磁场Ⅰ中运动时,受到重力和洛伦兹力,将尘粒的运动分解为水平和竖直两个方向,将洛伦兹力也分解为水平和竖直两个方向.
如图.
对水平方向用牛顿第二定律,得
Fx=max
qvyB=max=m△vx △t
则有qvyB△t=m△vx
∑qvyB△t=∑m△vx
得到qBy=mv
由题微粒恰好能进入Ⅱ区域时,则速度v与Ⅰ、Ⅱ界面平行
由动能定理,得mgy=
mv21 2
代入解得y=2m2g B2q
故欲使微粒能进入Ⅱ区域,区域Ⅰ宽度d应满足的条件d<
.2m2g B2q
答:(1)该尘粒在进入Ⅱ区域时的速率为
.2gd
(2)匀强电场的电场强度和匀强磁场的磁感应强度的大小为
.2m
sinα2gd qL
(3)欲使微粒能进入Ⅱ区域,区域Ⅰ宽度d应满足的条件是d<
.2m2g B2q
