问题
问答题
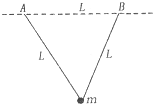
如图所示,两段长均为L的轻质线共同系住一个质量为m的小球,另一端分别固定在等高的A、B两点,A、B两点间距也为L,今使小球在竖直平面内做圆周运动,当小球到达最高点的速率为v时,两段线中张力恰好均为零,若小球到达最高点速率为2v,则此时每段线中张力为多少?(重力加速度为g)
答案
当速率为v时,则有mg=m
①v2 r
当速率为2v时,则有mg+F=m
②(2v)2 r
联立①②得,F=3mg
设每根线上的张力为T,满足:
2Tcos30°=F
即得T=
mg3
答:此时每段线中张力为
mg.3
