问题
解答题
一个三位数，十位上的数字是百位上数字的2倍，十位上的数字比个位上的数字大1.
（1）若设百位上的数字为a，则个位数字为 ，这个三位数可表示为 ；
（2）这个三位数能被5整除吗？若能，求出这个三位数；若不能请说明理由.
答案
（1）
,
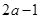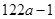（2）能，这个三位数为365.
题目分析：（1）用字母表示各数位的数，在写这个三位数时，百位上的字母要乘以100，十位上要乘以10；（2）能被5整除的数的特点是：个位数要么是5，要么是0.
试题解析：（1）设百位上的数字为a ，所以十位上的数字是2 a，又因为十位上的数字比个位上的数字大1，所以个位数字为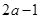；所以这个三位数为：
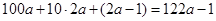；（2）这个三位数如果能被5整除，则个位数必须是5或0，若
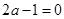，则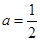
，a是分数，不符合实际要求. 若
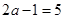，则a=3，这时这个三位数是365.