问题
计算题
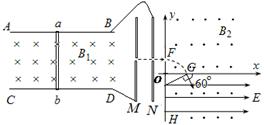
如图所示，AB、CD是处在方向垂直纸面向里、磁感应强度为B1的匀强磁场的两条金属导轨（足够长），导轨宽度为d，导轨通过导线分别与平行金属板MN相连，有一与导轨垂直且始终接触良好的金属棒ab以某一速度
沿着导轨做匀速直线运动。在y轴的右方有一磁感应强度为B2的方向垂直纸面向外的匀强磁场，在x轴的下方有一场强为E的方向平行x轴向右的匀强电场。现有一质量为m、电荷量为q的带正电粒子在M板由静止经过平行金属板MN，然后以垂直于y轴的方向从F处沿直线穿过y轴，而后从x轴上的G处以与x轴正向夹角为60°的方向进入电场和磁场叠加的区域，最后到达y轴上的H点。已知OG长为l，不计粒子的重力。求：
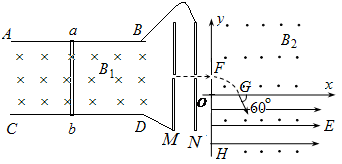
（1）金属棒ab做匀速直线运动速度的大小B？
（2） 粒子到达H点时的速度多大？
（3）要使粒子不能回到y轴边界， 电场强度以满足什么条件？
答案
见题目分析
题目分析： 解：金属棒ab在切割磁感线过程中产生的感应电动势为：
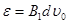（2分）
设粒子在F进入磁场时的速度为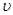
，由牛顿第二定律得：
（2分）
由几何知识可得（如图）
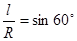（2分）
粒子在通过MN过程中由动能定理得：
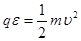（2分）
联解以上各式得：
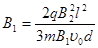（2分）
（2）从D到C只有电场力对粒子做功，电场力做功与路径无关，根据动能定理，有
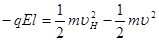， （2分）
解得：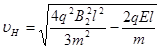
（2分）
（3）
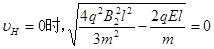（1分）
要使粒子不能回到y轴边界，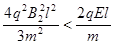
（2分）
即 
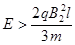（1分）
