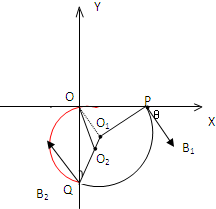
如图所示,在平面直角坐标系XOY内,第I象限存在沿Y轴正方向的匀强电场,第IV象限内存在垂直于坐标平面向里的匀强磁场,磁感应强度大小设为B1(未知),第III象限内也存在垂直于坐标平面向里的匀强磁场B2(未知).一质量为m的电子(电量为e,不计重力),从Y轴正半轴上Y=h处的M点,以速度v0垂直于Y轴射入电场,经X轴上X=
h处的P点进入第IV象限磁场,然后从Y轴上Q点进入第III象限磁场,OQ=OP,最后从O点又进入电场.2 3 3
(1)求匀强电场的场强大小E;
(2)求粒子经过Q点时速度大小和方向;
(3)求B1与B2之比为多少.

(1)电子在电场中做类平抛运动,则
x=v0t=2 3
h3
h=
at21 2
又由牛顿第二定律得 a=eE m
解得:E=3mv02 2eh
(2)画出电子在磁场中运动的轨迹图,
vy=at=
v03
∴v=
=2v0
+v 20 v 2y
tanθ=
=vy v0 3
∴θ=60
∴∠OPO1=30° 又∵OQ=OP
由几何关系得∠OQO1=∠OPO1=30°
∴粒子到达Q点时速度方向与y轴正向成60°
(3)由几何关系得 r1cos30°+r1sin30°=op=2 3
h3
∴r1=(2-2 3
)h3
又r1=
=mv eB1
进入B2后,2mv0 eB1
由几何关系得:2r2cos30°=OQ=OP=2 3
h3
∴r2=
h2 3
又r2=
∴2mv0 eB2
=B1 B2
=r2 r1 3+ 3 6
答:
(1)匀强电场的场强大小E是
;3m v 20 2eh
(2)粒子经过Q点时速度大小为2v0,方向与y轴正向成60°;
(3)B1与B2之比为
.3+ 3 6
