问题
问答题
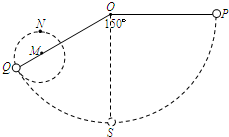
用长为L的细线系一个质量为m的小球(小球可以视为质点),线的一端固定在空间的O点.先将小球拉至图中的P位置,使OP水平,然后无初速释放小球.当小球绕O点转动150°到达Q位置时,细线碰到了一个固定的细钉子M,此后小球开始绕M做圆周运动.已知OM的长度是
,求:4L 5
(1)小球到达O点正下方的S点时细线对小球的拉力F1多大?
(2)小球到达Q位置时的速度v1多大?
(3)小球通过最高点N时细线对小球的拉力F2是多大?
答案
(1)从P到S的过程根据机械能守恒定律得:
mvS2=mgL1 2
在S点有:
F1-mg=mv2 L
解得:F1=3mg
(2)碰到钉子时线速度大小不变,从P到Q运用机械能守恒定律得:
mvQ2=mgLcos60°1 2
解得:vQ=gL
(3)根据机械能守恒定律得:
mvN2=(1 2
Lcos60°-4 5
L)mg1 5
又有:F2+mg=mvN2
L1 5
联立解得:F2=mg
答:(1)小球到达O点正下方的S点时细线对小球的拉力F1为3mg;
(2)小球到达Q位置时的速度v1为gL
(3)小球通过最高点N时细线对小球的拉力F2是mg.
