如图所示，光滑斜面末端与一个半径为R的光滑圆轨道平滑连接，一

问题问答题

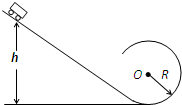
如图所示，光滑斜面末端与一个半径为R的光滑圆轨道平滑连接，一质量为m的小车（大小可忽略）小车从斜面上的某一高度由静止滑下，小车沿圆环轨道运动恰能越过圆弧轨道最高点．已知重力加速度为g．求：

（1）小车在圆轨道最低点时的速度．

（2）小车下滑的高度h．

答案

（1）小车恰能越过圆轨道的最高点，它越过圆轨道的最高点的速度为v₀，由牛顿第二定律得：

mg=m

，

解得：v₀=

小车在最低点时的速度为v₁，由机械能守恒定律得：

mv₀²+2mgR=

mv²_{1
解得：v₁=
5gR
（2）设两车滑到圆轨道最低点时的速度为v，由机械能守恒定律得：
1
2
mv²₁=mgh
小车下滑时高度h=
5
2
R
答：（1）小车在圆轨道最低点时的速度是
5gR
．
（2）小车下滑的高度是
5
2
R．}