问题
计算题
（15分） 光滑的平行金属导轨长x＝2 m，两导轨间距L＝0.5 m，轨道平面与水平面的夹角θ＝30°，导轨上端接一阻值为R＝0.6 Ω的电阻，轨道所在空间有垂直轨道平面向上的匀强磁场，磁场的磁感应强度B＝1 T，如图所示．有一质量m＝0.5 kg、电阻r＝0.4 Ω的金属棒ab，放在导轨最上端，其余部分电阻不计．已知棒ab从轨道最上端由静止开始下滑到最底端脱离轨道的过程中，电阻R上产生的热量Q1＝0.6 J，取g＝10 m/s2，试求：
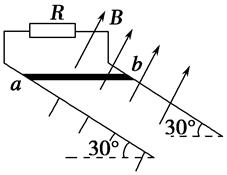
（1）当棒的速度v1＝2 m/s时，电阻R两端的电压；
（2）棒下滑到轨道最底端时速度的大小；
（3）棒下滑到轨道最底端时加速度a的大小．
答案
⑴ 0.6V ⑵ 4m/s ⑶
题目分析：（1） E＝Blv＝1 V
I＝
＝1 A，
U＝IR＝0.6 V.
（2）根据Q＝I2Rt得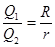
，
金属棒中产生的热量Q2＝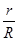
Q1＝0.4 J
设棒到达最底端时的速度为v2，根据能的转化和守恒定律，有：
mgLsin θ＝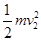
＋Q1＋Q2，解得：v2＝4 m/s。
⑶ 棒到达最底端时，回路中产生的感应电流为：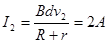
根据牛顿第二定律：mgsinθ－BI2d="ma"
解得：a=3m/s2
。
。