问题
计算题
(17分)如图所示,光滑导轨abc与fed相距l=0.1m,其中ab、fe段是倾角θ=60°的直轨道,bc、ed段是半径r=0.6m的圆弧轨道且与ab、fe相切,轨道末端c、d点切线与一放置在光滑水平地面上、质量M=2kg的木板上表面平滑连接。在abef间有垂直于轨道平面向下、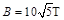 的匀强磁场,定值电阻R=1Ω。把质量为m=1kg、电阻不计的金属杆从距b、e高h=1m的导轨上静止释放,杆在直轨道上先加速后匀速下滑。如果杆与木板间摩擦因数μ=0.2,取g=10m/s2,求:
的匀强磁场,定值电阻R=1Ω。把质量为m=1kg、电阻不计的金属杆从距b、e高h=1m的导轨上静止释放,杆在直轨道上先加速后匀速下滑。如果杆与木板间摩擦因数μ=0.2,取g=10m/s2,求:
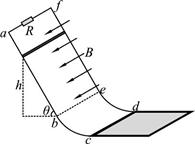
(1)杆运动到cd时对轨道的压力F大小及杆由静止下滑到cd的过程中R上产生的焦耳热Q;
(2)要使杆不从木板上掉下的木板最小长度s。
答案
见题目分析
题目分析:(1)设杆滑到be处时速度为v1,由题意知此时杆匀速下滑,有:
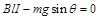 ①
①
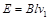 ②
②
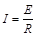 ③
③
由能量守恒:
|
 ④设杆滑到cd处时速度为v2,杆受到轨道支持力为F′,由动能定理有:
④设杆滑到cd处时速度为v2,杆受到轨道支持力为F′,由动能定理有: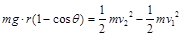 ⑤
⑤
cd处: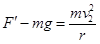 ⑥
⑥
由牛顿第三定律: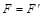 ⑦
⑦
联解①②③④⑤⑥⑦并代入数据得:
F′=25N ⑧
Q=8.5J ⑨
(2)杆滑上木板后,杆与木板在相互间摩擦力作用下运动,设经过时间t共同运动,则:
对杆: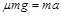 ⑩
⑩
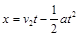 ⑪
⑪
对木板: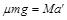 ⑫
⑫
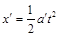 ⑬
⑬
共同运动时:
 ⑭
⑭
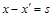 ⑮
⑮
联解⑩⑪⑫⑬⑭⑮并代入数据得:
s=1.5m ⑯
评分参考意见:本题满分17分,其中④式2分,①②③⑤⑥⑦⑧⑨⑩⑪⑫⑬⑭⑮⑯式各1分;若有其他合理解法且答案正确,可同样给分。
