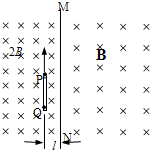我国科学家在对放射性元素的研究中,进行了如下实验:如图所示,以MN为界,左、右两边分别是磁感应强度为2B和B的匀强磁场,且磁场区域足够大.在距离界线为l处平行于MN固定一个长为s光滑的瓷管PQ,开始时一个放射性元素的原子核处在管口P处,某时刻该原子核平行于界线的方向放出一质量为m、带电量-e的电子,发现电子在分界线处速度方向与界线成60°角进入右边磁场,反冲核在管内匀速直线运动,当到达管另一端Q点时,刚好又俘获了这个电子而静止.求:
(1)电子在两磁场中运动的轨道半径大小(仅用l表示)和电子的速度大小;
(2)反冲核的质量.
由题意知有两种可能轨迹,分别如图甲、乙所示.
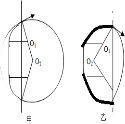
对于图甲所示情况:
(1)R1=l+R1sin30°
∴R1=2l
由R1=,R2=
得R2=2R1=4l
解得 v=
(2)运行时间:t=2×T1+T2=2××+×=
反冲核的速度V==
由动量守恒mv-MV=0
得反冲核的质量M==
[或将s=2(R2sin60°-R1sin60°)=2l代入得M=
对于图乙所示情况:
由图乙可得l=R1+R1sin30° R1=l,
由R1=,R2=
得R2=2R1=l
v=
(2)运行时间:t=2×T1+T2=2××+×=
反冲核的速度V==
由动量守恒mv-MV=0
得反冲核的质量M==
(或将s=2R1cos30°=l代入得M=)
答:(1)电子在两磁场中运动的轨道半径大小为2l和4l,或为l和l.电子的速度为或.
(2)反冲核的质量为或.