(20分)足够长的平行金属导轨ab、cd放置在水平面上,处在磁感应强度B=1.00T的竖直方向的匀强磁场中,导轨间连接阻值为R=0.30Ω的电阻,质量m=0.5kg的金属棒ef与bc紧贴在导轨上,处于两导轨间的长度L=0.40m、电阻r=0.10Ω,如图所示。在水平恒力F作用下金属棒ef由静止开始向右运动,其运动距离与时间的关系如下表所示。导轨与金属棒ef间的动摩擦因数为0.3,导轨电阻不计,g=10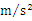 求:
求:

| 时间t(s) | 0.0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 | 7.0 |
| 运动距离x(m) | 0.0 | 0.6 | 2.0 | 4.3 | 6.8 | 9.3 | 11.8 | 14.3 |
(2)水平恒力F;
(3)庆丰同学在计算7.0s时间内,整个回路产生的焦耳热Q时,是这样计算的:
先算7.0s内的电荷量
再算电流
再用公式 计算出焦耳热
计算出焦耳热
请你简要分析这样做是否正确?认为正确的,请算出结果;认为错误的,请用自己的方法算出7.0s,整个回路产生的焦耳热Q。
(1)6.8C (2)2.5N (3)12.7J
题目分析:(1).金属棒产生的平均感应电动势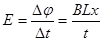 (1分)
(1分)
平均电流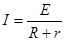 (1分)
(1分)
电荷量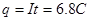 (2分)
(2分)
(2).由表中数据可知3.0s以后棒ef做匀速直线运动
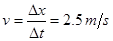 (2分)
(2分)
F-f=BIL (2分)
由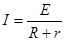 , E= BLv (2分)
, E= BLv (2分)
解得F="BIL+" f=2.5N (3分)
(3)庆丰同学用电流的平均值计算焦耳热是错误的, (2分)
根据能量转化和守恒定律有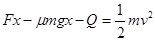 (3分)
(3分)
解得Q=12.7J (2分)
