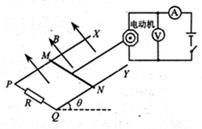
如图,电阻不计的足够长的平行光滑金属导轨PX、QY相距L=0.5m,底端连接电阻R=2Ω,导轨平面倾斜角θ=30°,匀强磁场垂直于导轨平面向上,磁感应强度B=1T。质量m=40g、电阻R=0.5Ω的金属棒MN放在导轨上,金属棒通过绝缘细线在电动机牵引下从静止开始运动,经过时间t1=2s通过距离x=1.5m,速度达到最大,这个过程中电压表示数U0=8.0V,电流表实数I0=0.6A,示数稳定,运动过程中金属棒始终与导轨垂直,细线始终与导轨平行且在同一平面内,电动机线圈内阻r0=0.5Ω,g=10m/s2.。求:
(1)细线对金属棒拉力的功率P多大?
(2)从静止开始运动的t1=2s时间内,电阻R上产生的热量QR是多大?
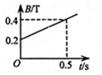
(3)用外力F代替电动机沿细线方向拉金属棒MN,使金属棒保持静止状态,金属棒到导轨下端距离为d=1m。若磁场按照右图规律变化,外力F随着时间t的变化关系式?
(1)0.3W;(2)0.224J;(3)F =" 0.016t" + 0.208(N)
题目分析:(1)根据能量转化和守恒,有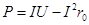 解得 P =" 0.3W"
解得 P =" 0.3W"
(2)当从静止开始运动经过t1=2s时间,金属棒速度达到最大,设此时为vm,金属棒中电动势为E,电流为I1,受到的安培力为F安,细线的拉力为F拉,则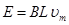 ,
,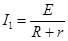
F安= BI1L
P =F拉vm
F拉 =" mgsinθ" + F安
解得 vm= 1m/s
金属棒从静止开始运动到达到最大速度过程中,设整个电路中产生的热量为Q,由能量转化和守恒得
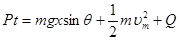
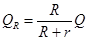
解得 QR=0.224J
(3)由图可知 
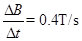
设在t时刻,磁场的磁感应强度为B',金属棒中电动势为E',电流为I',受到的安培力为
F安',则
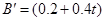 (T)
(T)
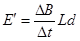 ,
,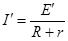
F安' =B' I'L
 F安'
F安'
解得 F =" 0.016t" + 0.208(N)
