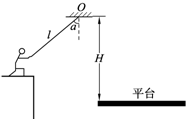
“快乐向前冲”节目中有这样一种项目,选手需要借助悬挂在高处的绳飞跃到鸿沟对面的平台上,如果已知选手的质量为m,选手抓住绳由静止开始摆动,此时绳与竖直方向夹角为α,绳的悬挂点O距平台的竖直高度为H,绳长为l,不考虑空气阻力和绳的质量,下列说法正确的是( )
A.选手摆到最低点时处于失重状态
B.选手摆到最低点时所受绳子的拉力为(3-2cosα)mg
C.选手摆到最低点时所受绳子的拉力大小大于选手对绳子的拉力大小
D.选手摆到最低点的运动过程中,其运动可分解为水平方向的匀加速运动和竖直方向上的匀加速运动
A、失重时物体有向下的加速度,超重时物体有向上的加速度,选手摆到最低点时向心加速度竖直向上,因此处于超重状态,故A错误;
B、摆动过程中机械能守恒,有:mgl(1-cosθ)=
mv2 ①1 2
设绳子拉力为T,在最低点有:T-mg= m
②v2 l
联立①②解得:T=(3-2cosα)mg,故B正确;
C、绳子对选手的拉力和选手对绳子的拉力属于作用力和反作用力,因此大小相等,方向相反,故C错误;
D、选手摆到最低点的运动过程中,沿绳子方向有向心加速度,沿垂直绳子方向做加速度逐渐减小的加速运动,其运动不能分解为水平方向的匀加速运动和竖直方向上的匀加速运动,故D错误.
故选B.
