问题
问答题
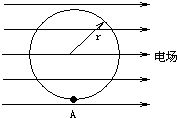
半径为r的绝缘光滑圆环固定在竖直平面内,环上套有一质量为m、带正电的珠子,空间存在水平向右的匀强电场,如图所示.珠子所受静电力是其重力的3/4倍.将珠子从环上最低位置A点静止释放,求:
(1)珠子所能获得的最大动能和在最大动能处环对珠子的作用力;
(2)要使珠子恰好能绕圆环做完整的圆周运动,则应在A点给珠子以多大的初速度?
答案

(1)珠子的平衡位置和圆心连线与竖直方向的夹角θ有tanθ=
=qE mg 3 4
珠子在平衡位置速度最大,珠子从A点运动到平衡位置,
由动能定理qErsinθ-mgr(1-cosθ)=
mv2=Ek1 2
最大动能 Ek=
qEr-mgr(1-3 5
)=4 5
-9mgr 20
=mgr 5
mgr1 4
在动能最大处圆环对珠子的作用力;
根据圆周运动N-mgcosθ-qEsinθ=mv2 r
得:N=
mg7 4
(2)如图,此时珠子做圆周运动的“最高点”为D,在D点,珠子速度为零,
从A点到D点过程,由动能定理
-mgr(1+cosθ)-qErsinθ=0-
m1 2 v 2A
得:vA=3 2gr 2
答:(1)珠子所能获得的最大动能
mgr和在最大动能处环对珠子的作用力1 4
mg;7 4
(2)要使珠子恰好能绕圆环做完整的圆周运动,则应在A点给珠子以3 2
的初速度.2gr
