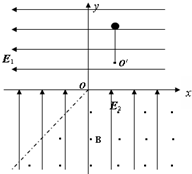
如图所示,在x轴上方有水平向左的匀强电场E1,在x轴下方有竖直向上的匀强电场E2,且E1=E2=5N/C,在图中虚线(虚线与y轴负方向成45°角)的右侧和x轴下方之间存在着垂直纸面向外的匀强磁场,磁感应强度B=2T.有一长L=5
m的不可伸长的轻绳一端固定在第一象限内的O'点,另一端拴有一质量M=0.1kg、带电量q=+0.2C的小球,小球可绕O'点在竖直平面内转动,OO'间距为L,与x轴正方向成45°角.先将小球放在O'正上方且绳恰好伸直的位置处由静止释放,当小球进入磁场前瞬间绳子绷断.重力加速度g取10m/s2.求:2
(1)小球刚进入磁场区域时的速度.
(2)细绳绷紧过程中对小球的弹力所做的功.
(3)小球从进入磁场到小球穿越磁场后第一次打在x轴上所用的时间及打在x轴上点的坐标.
(1)小球先做匀加速直线运动,直到绳子绷直,设绳绷紧前瞬间速度为v,绳子刚绷紧后小球速度大小为v2,进入有磁场的区域时速度的大小为v3,
则 v2=2ax

而 F合=
mg=ma2
又小球运动的位移为 x=
L 2
绳子绷紧后:v2=vcos45°
由动能定理:Mg•
L-qE1(L-2 2
L)=2 2
M1 2
-v 23
M1 2 v 22
联立解得:v3=10
m/s 2
(2)设细绳绷紧过程中对小球的弹力所做的功为W,根据动能定理得
W=1 2
-Mv 22
Mv21 2
解得,W=-5
J2
(3)小球进入磁场后,由于qE2=Mg,小球做匀速圆周运动,由洛伦兹力提供向心力,由牛顿第二定律得
qv3B=mv 23 R
得 R=
=Mv3 qB
m,T=5 2 2
=2πM qB
sπ 2
小球在运动半周后以v3出磁场,做匀速直线运动直到打到x轴上
匀速运动的时间t=
,小球从进入磁场到小球穿越磁场后第一次打在x轴上运动的总时间2R v3
t总=t+
=(0.5+T 2
)S=1.3sπ 4
小球打到x轴上的位置坐标为(-10m,0)
答:
(1)小球刚进入磁场区域时的速度是10
m/s.2
(2)细绳绷紧过程中对小球的弹力所做的功是-5
J.2
(3)球从进入磁场到小球穿越磁场后第一次打在x轴上所用的时间是1.3s,打在x轴上点的坐标为(-10m 0).
