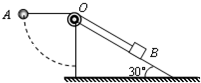
如图所示,倾角为30°的斜面体固定在水平地面上,一根不可伸长的轻绳两端分别系着小球A和物块B,跨过固定于斜面体顶端的滑轮O(可视为质点).A的质量为m,B的质量为4m.开始时,用手托住A,使OA段绳恰处于水平伸直状态(绳中无拉力),OB绳平行于斜面,此时B静止不动.将A由静止释放,在其下摆过程中B始终保持静止.则在绳子到达竖直位置之前,下列说法正确的是( )
A.物块B受到的摩擦力一直沿着斜面向上
B.物块B受到的摩擦力先减小后增大
C.绳子的张力先减小后增大
D.地面对斜面体的摩擦力方向一直水平向右
A、B、:初始情况下分析物块B受力:竖直向下的重力4mg、垂直斜面向上的支持力FN、沿斜面向上的静摩擦力Ff.沿斜面和垂直斜面正交分解B物块受到的力,
∴B物块处于平衡状态,则有:沿斜面方向:Ff=4mgsin30°=2mg,
垂直斜面方向:FN=4mgcos30°= 2
mg.3
由牛顿第三定律知:物块B对斜面有垂直斜面向下的压力
和沿斜面向下的静摩擦力F ′N
,把这两个力向水平方向分解,则得:斜面体水平方向受到B的作用力(取水平向左为正方向):F ′f
sin30°-F ′N
cos30°F ′f
又∴
'=FN=4mgcos30°=2F ′N
mg,3
=Ff=4mgsin30°=2mg.∴F ′f
sin30°-F ′N
cos30°=F ′f
mg- 3
mg=0,3
所以初始状态下斜面体水平方向受物块B的合力为零,不存在受地面的摩擦力.
小球A下摆过程中,物块B始终保持静止,则小球A不对外做功,机械能守恒,小球A的速度不断增大,到最低点时速度最大,这时小球A摆到低时对绳的拉力最大,设r为A到滑轮的绳长,最低点小球A的速度为v,则由机械能守恒定律得:
=mgr,又由牛顿第二定律得:F-mg=mv2 2
,∴小球A对绳的拉力为F=mv2 r
+mg=3mg,此时物块B在平行于斜面方向所受的摩擦力为mv2 r
=F-4mgsin30°=3mg-2mg=mg,方向沿斜面向下,由此可知物块B受到斜面的摩擦力先是沿斜面向上2mg,后逐渐减少到零,再沿斜面向下逐渐增大到mg,所以,选项A错误,选项B正确.F ″f
C:由以上分析知绳子的张力一直增大,小球A摆到低时对绳的拉力最大,所以,选项C错误.
D:将A由静止释放,在其下摆过程中B始终保持静止,在绳子到达竖直位置之前,把斜面与物块B看做整体,绳子始终有拉力,此拉力水平向左有个分力,而整体保持静止,水平方向受力平衡,因此,地面对斜面体的摩擦力方向一直水平向右,那么,选项D正确.
故选:B、D.
