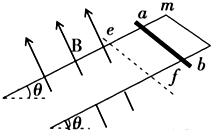
如图所示,两足够长的平行光滑金属导轨倾斜放置,与水平面间的夹角为θ=37°,两导轨之间距离为L=0.2m,导轨上端m、n之间通过导线连接,有理想边界的匀强磁场垂直于导轨平面向上,虚线ef为磁场边界,磁感应强度为B=2.0T.一质量为m=0.05kg的光滑金属棒ab从距离磁场边界0.75m处由静止释放,金属棒接入两轨道间的电阻r=0.4Ω,其余部分的电阻忽略不计,ab、ef均垂直导轨.(取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
(1)ab棒最终在磁场中匀速运动时的速度;
(2)ab棒运动过程中的最大加速度.
(1)ab受到的安培力F=BIL=
,B2L2v r
ab做匀速直线运动,由平衡条件得:
=mgsinθ,解得:v=0.75m/s;B2L2v r
(2)从ab棒开始运动到刚进入磁场过程中,
由机械能守恒定律得:mgssinθ=
mv′2,1 2
解得:v′=3m/s,
此时ab棒受到的安培力:
F′=
=B2L2v′ r
=1.2N,22×0.22×3 0.4
重力沿斜面方向的分力:G1=mgsinθ=0.3N,
F′>G1,ab棒进入磁场后做减速运动,
受到的安培力减小,当安培力与重力的分力相等时做匀速运动,
因此当ab棒刚进入磁场时加速度最大,
由牛顿第二定律得:F′-G1=ma,
解得:a=18m/s2,方向平行于斜面向上;
答:(1)ab棒最终在磁场中匀速运动时的速度为0.75m/s;(2)ab棒运动过程中的最大加速度大小为18m/s2,方向沿导轨斜面向上.
