在竖直平面内建立一平面直角坐标系xoy,x轴沿水平方向,如图甲所示.第二象限内有一水平向右的匀强电场,场强为E1.坐标系的第一、四象限内有一正交的匀强电场和匀强交变磁场,电场方向竖直向上,场强E2=
,匀强磁场方向垂直纸面.处在第三象限的某种发射装置(图中没有画出)竖直向上射出一个比荷E1 2
=102C/kg的带正电的微粒(可视为质点),该微粒以v0=4m/s的速度从-x上的A点进入第二象限,并以v1=8m/s速度从+y上的C点沿水平方向进入第一象限.取微粒刚进入第一象限的时刻为0时刻,磁感应强度按图乙所示规律变化(以垂直纸面向外的磁场方向为正方向),g=10m/s2.试求:q m
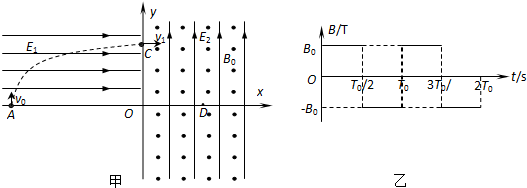
(1)带电微粒运动到C点的纵坐标值h及电场强度E1;
(2)+x轴上有一点D,OD=OC,若带电微粒在通过C点后的运动过程中不再越过y轴,要使其恰能沿x轴正方向通过D点,求磁感应强度B0及其磁场的变化周期T0为多少?
(3)要使带电微粒通过C点后的运动过程中不再越过y轴,求交变磁场磁感应强度B0和变化周期T0的乘积B0 T0应满足的关系?
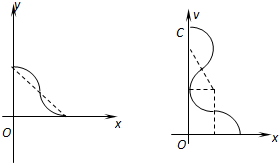
(1)将粒子在第二象限内的运动分解为水平方向和竖直方向,在竖直方向上做竖直上抛运动,在水平方向上做匀加速直线运动.
t=
=0.4s.v0 g
h=
t=0.8m.v0 2
ax=
=2g,v1 t
则qE1=2mg,解得E1=0.2N/C.
(2)qE2=mg,所以带电的粒子在第一象限将做匀速圆周运动,设粒子运动圆轨道半径为R,周期为T,则qv1B0=m
可得R=v12 R
.0.08 B0
使粒子从C点运动到D点,则有:h=(2n)R=(2n)
.0.08 B0
解得:B0=0.2n(T)(n=1,2,3…).
T=
.2πm qB0
=T0 2
,T 4
T0=
=T 2
=πm qB0
(s) (n=1,2,3…).π 20n
(3)当交变磁场周期取最大值而粒子不再越过y轴时可作如图运动情形:
由图可知θ=5π 6
T0≤
T=5 6
.5π 300B0
B0T0≤
(kg/C).π 60
答:(1)带电微粒运动到C点的纵坐标值h为0.8m.电场强度E1为0.2N/C.
(2)磁感应强度B0为B0=0.2n(T)(n=1,2,3…).磁场的变化周期T0为T0=
=T 2
=πm qB0
(s) (n=1,2,3…).π 20n
(3)交变磁场磁感应强度B0和变化周期T0的乘积B0 T0应满足B0T0≤
(kg/C).π 60
