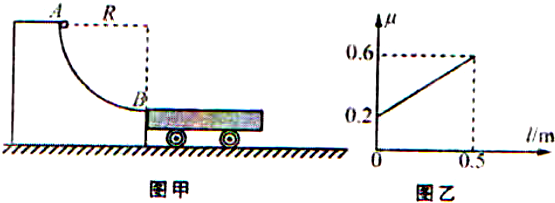
如图所示，半径R=0.45m的光滑14圆弧轨道固定在竖直平面内，B为轨

问题问答题

如图所示，半径R=0.45m 的光滑

圆弧轨道固定在竖直平面内，B为轨道的最低点，B点右侧的光滑的水平面上紧挨B点有一静止的 * * 板车，平板车质量M=2kg，长度为 0.5m，小车的上表面与B点等高，距地面高度为0.2m．质量 m=1kg 的物块（可视为质点）从圆弧最高点A由静止释放．g 取10m/s²．试求：

（1）物块滑到轨道上的B点时对轨道的压力；

（2）若将平板车锁定并且在上表面铺上一种特殊材料，其动摩擦因数从左向右随距离均匀变化如图乙所示，求物块滑离平板车时的速度；

（3）若撤去平板车的锁定与上表面铺的材料，此时物块与木板间的动摩擦因数为

，物块仍从圆弧最高点A由静止释放，请通过分析判断物块能否滑离平板车．若不能，请算出物块停在距平板车左端多远处；若能，请算出物块落地时距平板车右端的水平距离．

答案

（1）物体从圆弧轨道顶端滑到B点的过程中，机械能守恒，则

mgR=

mvB2，解得v_B=3m/s．

在B点由牛顿第二定律得，N-mg=m

vB2

解得N=mg+m

vB2

=30N

即物块滑到轨道上B点时对轨道的压力N′=N=30N，方向竖直向下．

（2）物块在小车上滑行时的摩擦力做功Wf=-

μ1mg+μ2mg

l=-2J

从物体开始滑到滑离平板车过程中由动能定理得，mgR+Wf=

mv2

解得v=

m/s

（3）当平板车不固定时，对物块a1=μg=

m/s2．

对平板车a2=

μmg

m/s2

设物块与平板车经过时间t达到共同速度（物块在平板车最左端的速度v_C=v_B），有

v_c-a₁t=a₂t，解得t=

此时△s=vct-

a1t2-

a2t2=

m＞0.5m，所以物块能滑离平板车．

设经过时间t₁物块滑离平板车，则vct1-

a1t12-

a2t12=0.5m

解得t1=

s（另一解t2=

s＞

s舍去）

物块滑离平板车时的速度v_物=v_c-a₁t₁=

m/s．

此时平板车的速度v车=a2t1=

m/s．

物块滑离平板车做平抛运动的时间t3=

=0.2s

物块落地时距平板车右端的水平距离x=（v_物-v_车）t₃=0.2m．

答：（1）物块滑到轨道上的B点时对轨道的压力为30N．

（2）物块滑离平板车时的速度

m/s．

（3）能滑离平板车，物块落地时距平板车右端的水平距离为0.2m．