问题
问答题
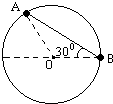
一光滑圆环固定在竖直平面内,环上套着两个小球A和B(中央有孔),A、B间由细绳连接着,它们处于如图中所示位置时恰好都能保持静止状态.此情况下,B球与环中心O处于同一水平面上,AB间的细绳呈伸直状态,与水平线成30°夹角.已知B球的质量为m,求:
(1)细绳对B球的拉力和A球的质量;
(2)剪断细绳后,B球运动到圆环最低点时对圆环的压力.
答案
(1)对B球,受力分析如图所示.Tsin30°=mg
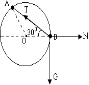
∴T=2mg①
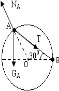
对A球,受力分析如图所示.在水平方向Tcos300=NAsin300…..②
在竖直方向NAcos300=mAg+Tsin300…③
由以上方程解得:mA=2m…④
(2)设B球第一次过圆环最低点时的速度为v,压力为N,圆环半径为r.
则 mgr=
mv2…⑥1 2
N-mg=m
…⑦v2 r
⑥⑦联解得:N=3mg…⑧
由牛顿第三定律得B球对圆环的压力 N′=N=3mg 方向竖直向下 ⑨
答:(1)细绳对B球的拉力为2mg,A球的质量为2m.
(2)剪断细绳后,B球运动到圆环最低点时对圆环的压力为3mg.
