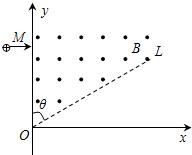
如图所示,虚线OL与y轴的夹角为θ=60°,在此角范围内有垂直于xOy平面向外的匀强磁场,磁感应强度大小为B.一质量为m、电荷量为q(q>0)的粒子从左侧平行于x轴射入磁场,入射点为M.粒子在磁场中运动的轨道半径为R.粒子离开磁场后的运动轨迹与x轴交于P点(图中未画出),且=R.不计重力.求M点到O点的距离和粒子在磁场中运动的时间.
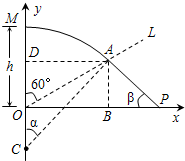
根据题意,粒子进入磁场后做匀速圆周运动,设运动轨迹交虚线OL于A点,圆心在y轴上的C点,AC与y轴的夹角为α;粒子从A点射出后,运动轨迹交x轴的P点,设AP与x轴的夹角为β,如右图所示
由牛顿第二定律得:qvB=m ①
周期为T== ②
过A点作x、y轴的垂线,垂足分别为B、D.
由几何知识得=Rsinα,=cot60°,=cotβ,=+,α=β ③
联立得到 sinα+cosα=1
解得 α=30°,或α=90°
设M点到O点的距离为h,有 =Rsinα h=R-,=-=Rcosα-
联立得到 h=R-Rcos(α+30°)(1分)
解得 h=(1-)R(α=30°) 或 h=(1+)R(α=90°)
当α=30°时,粒子在磁场中运动的时间为t==
当α=90°时,粒子在磁场中运动的时间为t==
答:M点到O点的距离h=(1-)R或h=(1+)R;粒子在磁场中运动的时间为或.