问题
解答题
观察下列关于自然数的等式:
32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
…
根据上述规律解决下列问题:
(1)完成第四个等式:92—4×( )2=( );
(2)写出你猜想的第n个等式(用含n的式子表示),并验证其正确性.
答案
(1)4,17;
(2)第n个等式为:(2n+1)2-4n2=2(2n+1)-1,证明见解析.
题目分析:由①②③三个等式可得,被减数是从3开始连续奇数的平方,减数是从1开始连续自然数的平方的4倍,计算的结果是被减数的底数的2倍减1,由此规律得出答案即可.
试题解析:(1)32-4×12=5 ①
52-4×22=9 ②
72-4×32=13 ③
…
所以第四个等式:92-4×42=17;
(2)第n个等式为:(2n+1)2-4n2=2(2n+1)-1,
左边=(2n+1)2-4n2=4n2+4n+1-4n2=4n+1,
右边=2(2n+1)-1=4n+2-1=4n+1.
左边=右边,
∴(2n+1)2-4n2=2(2n+1)-1.

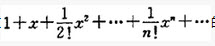 的收敛域为()。
的收敛域为()。