如图所示,直角坐标系xoy所决定的平面内,在平行于x轴的虚线MN上方、x<0的区域存在着沿x轴正方向的匀强电场;在x>0的某区域存在方向垂直于坐标平面的圆形有界匀强磁场(图中未画出).现有一比荷k=
=102C/kg的带正电粒子从虚线MN上的P处,以大小υ0=20m/s、方向平行于y轴的初速度射入电场,并恰好从原点O处射出,射出时的速度大小υ=40m/s,此后粒子先做匀速运动,然后进入圆形有界磁场,粒子从磁场中射出时,出射点为Q且射出时的速度方向沿y轴负方向.已知磁场的磁感应强度B=1.2T,不计粒子的重力,忽略粒子运动对电场、磁场的影响.求:q m
(1)粒子从O点射出时速度υ与y轴间的夹角θ.
(2)P、O两点间的电势差U.
(3)Q点的横坐标x.
(4)圆形有界匀强磁场的最小面积S.
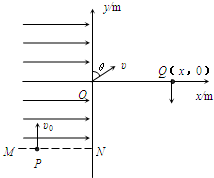
(1)带电粒子在匀强电场中y轴方向上做匀速直线运动,x轴方向上做匀加速直线运动,将O点的速度分解,有:
cosθ=
=v0 v
.1 2
解得θ=60°.
(2)根据动能定理得,qU=
mv2-1 2
mv021 2
因为比荷k=
=102C/kgq m
代入数据解得:U=6V.
(3)根据qvB=mv2 R
带电粒子在匀强磁场中的轨道半径:R=
=mv qB
×40 1.2
=1 100
m.1 3
根据几何关系得:x=R+
=3R=1m.R sin30°
(4)以粒子在匀强磁场中运动的轨迹的初末两点连线为圆的直径,该圆的面积为匀强磁场的最小面积.
该圆的半径r=Rsin60°=
×3 2
=1 3
m3 6
则S=πr2=
m2.π 12
答:(1)粒子从O点射出时速度υ与y轴间的夹角θ为60°.
(2)P、O两点间的电势差U为6V.
(3)Q点的横坐标x=1m.
(4)圆形有界匀强磁场的最小面积为
m2.π 12
