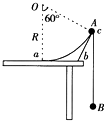
如图所示，圆心在O点，半径为R=0.24m的圆弧形支架abc竖直固定在

问题问答题

如图所示，圆心在O点，半径为R=0.24m的圆弧形支架abc竖直固定在水平桌面上，支架最低点a与桌面相切，最高点c与O点的连线Oc与Oa夹角为60°．一轻绳两端系着质量分别为m₁和m₂的小球A和B（均可视为质点），挂在圆弧边缘c的两边．开始时，A、B均静止，A的位置与c点等高，不计一切摩擦，连线和水平桌面足够长，g=10m/s²．

（1）为使A能沿圆弧下滑到a点，m₁与m₂之间必须满足什么关系？

（2）若m₁=3m₂，求A到达圆弧最低点a时，A的速度大小．

（3）若m₁=3m₂，求B能上升的最大高度．

答案

（1）A、B两球组成的系统机械能守恒，有：

m₁gR（1-cos60°）=m₂gR

解得m₁=2m₂．

（2）若m₁=3m₂，设A滑动最低点a时的速度为v_A，B的速度为v_B．

v_B=v_Acos30°

根据系统机械能守恒定律得，

m₁gR（1-cos60°）-m₂gR=

m1vA2+

m2vB2

解得v_A=0.8m/s．

（3）当A的速度减为零，B上升的高度最高．

根据系统机械能守恒定律得，

m₁gR（1-cos60°）=m₂gh

解得h=

=0.36m．

答：（1）为使A能沿圆弧下滑到a点，m₁与m₂之间必须满足m₁=2m₂．

（2）A的速度大小为0.8m/s．

（3）B能上升的最大高度为0.36m．