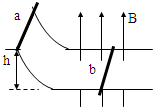
如图所示,光滑平行导轨仅其水平部分处于竖直向上的匀强磁场中,金属杆b静止在导轨的水平部分上,金属杆a沿导轨的弧形部分从离地h处由静止开始下滑,运动中两杆始终与轨道垂直并接触良好且它们之间未发生碰撞,已知a杆的质量ma=m0,b杆的质量mb=
m0,且水平导轨足够长.4 3
(1)a和b的最终速度分别是多大?
(2)整个过程中回路释放的电能是多少?
(3)若已知a、b杆的电阻之比Ra:Rb=3:4,其余电阻不计,则整个过程中a、b上产生的热量分别是多少?
(1)a棒由斜面下落过程中 magh=
mav121 2
解得:v1=2gh
在水平面上a、b最后以相同的速度匀速运动,根据动量守恒定律得 mav1=(ma+mb)v2
解得:v2=3 7 2gh
(2)全程由能量守恒得:E=magh-
(ma+mb)v22=1 2
m0gh4 7
(3)Ra、Rb串联由 Q=I2Rt 得 Qa=
E=3 7
m0ghQb=12 49
E=4 7
m0gh16 49
答:
(1)a和b的最终速度分别是
,2gh 3 7
.2gh
(2)整个过程中回路释放的电能是
m0gh.4 7
(3)若已知a、b杆的电阻之比Ra:Rb=3:4,其余电阻不计,则整个过程中a、b上产生的热量分别是
m0gh,12 49
m0gh.16 49
