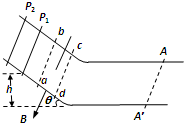
如图所示,金属导轨是由倾斜和水平两部分圆滑相接而成,倾斜部分与水平夹角θ=37°,导轨电阻不计.abcd矩形区域内有垂直导轨平面的匀强磁场,bc=ad=s=0.20m.导轨上端搁有垂直于导轨的两根相同金属杆P1、P2,且P1位于ab与P2的中间位置,两杆电阻均为R,它们与导轨的动摩擦因数μ=0.30,P1杆离水平轨道的高度h=0.60m,现使杆P2不动,让P1杆静止起滑下,杆进入磁场时恰能做匀速运动,最后P1杆停在AA′位置.
求:(1)P1杆在水平轨道上滑动的距离x;
(2)P1杆停止后,再释放P2杆,为使P2杆进入磁场时也做匀速运动,事先要把磁场的磁感应强度大小调为原来的多少倍?
(3)若将磁感应强度B调为原来3倍,再释放P2,问P2杆是否有可能与P1杆不碰撞?为什么?
(1)设杆的质量为m,则杆进入磁场时沿斜面方向受力平衡,受到的安培力
F=mgsinθ-μmgcosθ
对P1杆运动的全过程,根据动能定理:
mgh-μmgcosθ
-Fs-μmgx=0h sinθ
解得:x=
-hcotθ=0.96mh-(sinθ-μcosθ)s μ
(2)设杆长为l、进入磁场时速度为v,杆进入磁场能做匀速运动,满足:
BIl=mgsinθ-μmgcosθ
电流:I=Blv 2R
得:B=
可见B与2mgR(sinθ-μcosθ) vl2
成反比.v
设杆下滑加速度为a,由题意P1、P2杆到ab的距离可记为L、2L,则
=v1 v2
=2aL 2a.2L 1 2
可得磁感应强度调后B2与调前B1之比
=B2 B1
=0.84所以应调到原来的0.84倍v1 v2
(3)P2杆必与P1杆发生碰撞,因为此条件下,P2杆进入磁场后做加速度变小的减速运动,它离开磁场时的速度必大于P1杆离开磁场时的速度.
答:(1)P1杆在水平轨道上滑动的距离x=0.96m;(2)事先要把磁场的磁感应强度大小调为原来的0.84倍;
(3)P2杆必与P1杆发生碰撞,因为此条件下,P2杆进入磁场后做加速度变小的减速运动,它离开磁场时的速度必大于P1杆离开磁场时的速度.
