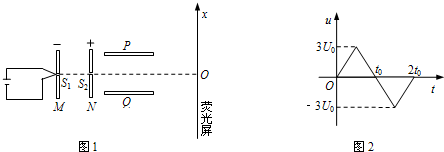
如图1所示,M、N为竖直放置的平行金属板,两板间所加电压为U0,S1、S2为板上正对的小孔.金属板P和Q水平放置在N板右侧,关于小孔S1、S2所在直线对称,两板的长度和两板间的距离均为l;距金属板P和Q右边缘l处有一荧光屏,荧光屏垂直于金属板P和Q;取屏上与S1、S2共线的O点为原点,向上为正方向建立x轴.M板左侧电子枪发射出的电子经小孔S1进入M、N两板间.电子的质量为m,电荷量为e,初速度可以忽略.不计电子重力和电子之间的相互作用.
(1)求电子到达小孔S2时的速度大小v;
(2)若板P、Q间只存在垂直于纸面向外的匀强磁场,电子刚好经过P板的右边缘后,打在荧光屏上.求磁场的磁感应强度大小B和电子打在荧光屏上的位置坐标x;
(3)若金属板P和Q间只存在电场,P、Q两板间电压u随时间t的变化关系如图2所示,单位时间内从小孔S1进入的电子个数为N.电子打在荧光屏上形成一条亮线.忽略电场变化产生的磁场;可以认为每个电子在板P和Q间运动过程中,两板间的电压恒定.
a.试分析在一个周期(即2t0时间)内单位长度亮线上的电子个数是否相同.
b.若在一个周期内单位长度亮线上的电子个数相同,求2t0时间内打到单位长度亮线上的电子个数n;若不相同,试通过计算说明电子在荧光屏上的分布规律.
(1)根据动能定理eU0=
mv2解得:v=1 2
①2eU0 m
(2)电子在磁场中做匀速圆周运动,设圆运动半径为 R,
在磁场中运动轨迹如图1,由几何关系R2=l2+(R-
)2l 2
解得:R=
l5 4
根据牛顿第二定律:Bev=mv2 R
解得:B=4 5l 2mU0 e
设圆弧所对圆心为α,满足:sinα=
=l R 4 5
由此可知:tanα=4 3
电子离开磁场后做匀速运动,满足几何关系:
=tanαx- l 2 l
通过上式解得坐标x=
l11 6
(3)a.设电子在偏转电场PQ中的运动时间为t1,PQ间的电压为u
垂直电场方向:l=vt1②
平行电场方向:x1=
at12 ③1 2
此过程中电子的加速度大小 a=
④eu ml
①、②、③、④联立得:x1=ul 4U0
电子出偏转电场时,在x方向的速度vx=at1 ⑤
电子在偏转电场外做匀速直线运动,设经时间t2到达荧光屏.则
水平方向:l=vt2 ⑥
竖直方向:x2=vxt2 ⑦
①、⑤、⑥、⑦联立,解得:x2=
电子打在荧光屏上的位置坐标x=x1+x2=ul 2U0
u ⑧3l 4U0
对于有电子穿过P、Q间的时间内进行讨论:

由图2可知,在任意△t时间内,P、Q间电压变化△u相等.
由⑧式可知,打在荧光屏上的电子形成的亮线长度△x=
△u.3l 4U0
所以,在任意△t时间内,亮线长度△x相等.
由题意可知,在任意△t时间内,射出的电子个数是相同的.
也就是说,在任意△t时间内,射出的电子都分布在相等的亮线长度△x范围内.
因此,在一个周期内单位长度亮线上的电子个数相同.
b.现讨论2t0时间内,打到单位长度亮线上的电子个数:
当电子在P、Q电场中的侧移量x1=
时,由x1=l 2
得:u=2U0ul 4U0
当偏转电压在0~±2U0之间时,射入P、Q间的电子可打在荧光屏上.
由图2可知,一个周期内电子能从P、Q电场射出的时间t=
T=2 3 4t0 3
所以,一个周期内打在荧光屏上的电子数Nt=4Nt0 3
由⑧式,电子打在荧光屏上的最大侧移量xm=3l 2
亮线长度L=2xm=3l
所以,从0~2t0时间内,单位长度亮线上的电子数n=
=Nt L 4Nt0 9l
答:
(1)电子到达小孔S2时的速度大小v为
;2eU0 m
(2)磁场的磁感应强度大小B是4 5l
,电子打在荧光屏上的位置坐标x为2mU0 e
l;11 6
(3)从0~2t0时间内,单位长度亮线上的电子数n为
.4Nt0 9l