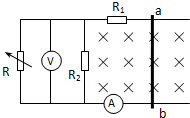
如图所示,两条平行的光滑水平导轨上,用套环连着一质量为0.2kg、电阻为2Ω的导体杆ab,导轨间匀强磁场的方向垂直纸面向里.已知R1=3Ω,R2=6Ω,电压表的量程为0~10V,电流表的量程为0~3A(导轨的电阻不计).求:
(1)将R调到30Ω时,用垂直于杆ab的力F=40N,使杆ab沿着导轨向右移动且达到最大速度时,两表中有一表的示数恰好满量程,另一表又能安全使用,则杆ab的速度多大?
(2)将R调到3Ω时,欲使杆ab运动达到稳定状态时,两表中有一表的示数恰好满量程,另一表又能安全使用,则拉力应为多大?
(3)在第(1)小题的条件下,当杆ab运动达到最大速度时突然撤去拉力,则电阻R1上还能产生多少热量?
(1)当R=30Ω时,R与R2的并联电阻阻值R′=5Ω,
假设电流表满偏,则U=IR′=3×5=15V>10V,
电压表不能正常工作,不符合题意;
电压表满偏时,电路电流:I1=
=U R′
=2A<3A,10V 5Ω
电流表能正常工作,则电压表满偏;
电路总电阻:R总=r+R1+R′=10Ω,
杆ab速度最大时,安培力与拉力相等,
由平衡条件得:BIL=F,BL=20N/A,
由欧姆定律得:I1=
=E1 R总
=BLv R总
=2v,20v 10
解得:v=1m/s;
(2)当R=3Ω时,R与R2并联值为R″=2Ω;
设电压表满偏,I=
=U R″
=5A,5A>3A,不符题意,说明电压表未满偏.10 2
电流表满偏,电路电流:I′=3A,
金属棒切割磁感线产生的电动势:E2=I′(r+R1+R″)=21V,
安培力F安=BI′L=BLI′=20×3=60N,
由平衡条件可知,拉力F′=F安=60N;
(3)撤去外力时杆ab具有动能:EK=
mv2=0.1J,1 2
该动能最后全部转化成电路中的热能,即Q=EK=0.1J;
设某时刻电阻R1上的电功率为P1,电路中的总功率为P,总电阻为R,
=P1 P
=Q1 Q
=0.3,Q1=0.3Q=0.03J; R1 R
答:(1)杆ab的速度为1m/s;
(2)拉力为60N;
(3)电阻R1上还能产生0.03J的热量.
