问题
问答题
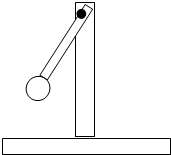
如图,一支架质量M=10kg,置于水平地面上,轴O处有一长为L=0.4m的杆(质量不计),杆的另一端固定一个质量为m=0.5kg的小球,使小球在竖直平面上做匀速圆周运动,支架保持静止.若小球到达最高点时,杆恰好对小球的作用力为O,取重力加速度g=10m/s2,求小球做圆周运动的速度大小和小球经过最低点时支架对地面的压力为多大?
答案
设小球的速度大小为v,由题意可知,在最高点时有:mg=mv2 L
解得:V=
=gL
m/s=2m/s10×0.4
设小球运动到最低点时向心力为T,根据牛顿第二定律,有:T-mg=mv2 L
解得:T=m
+mg=2mg v2 L
分析支架受力,根据牛顿第三定律可得支架对地面的压力N为:
N=Mg+T
代入数值计算,得:N=(M+2m)g=110N
答:小球做圆周运动的速度大小为2m/s,小球经过最低点时支架对地面的压力为110N.
