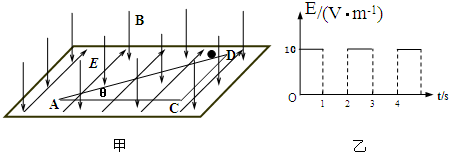
光滑绝缘水平面上固定一个光滑绝缘的斜劈，有一带电小球，质量m=

问题问答题

光滑绝缘水平面上固定一个光滑绝缘的斜劈，有一带电小球，质量m=1×10^-9kg，电荷量q=-6.28×10⁸C，小球紧靠在斜劈表面上，如图甲所示．空间充满相互垂直的匀强磁场和匀强电场，磁场方向竖直向下，磁感应强度大小为B=0.1T，电场沿水平方向且与斜劈底边垂直，电场强度大小按图乙所示规律变化，规定图示电场强度的方向为正方向．小球从t=0时刻由静止开始沿D→A方向滑动．已知sinθ=0.1045，cosθ=0.9945（算中取π=3.14，sinθ=0.1，cosθ=1）．求

（1）第1秒末粒子的速度大小

（2）第2秒内粒子离开斜边AD的最大距离

（3）第3秒内粒子能否离开斜劈？若能离开，离开时的速度多大？若不能离开，第3秒末的速度多大？

答案

（1）设第1秒末离开斜面，第1秒末的速度为v=at=

tsinθ=62.8m/s

此时电场力在垂直斜面方向的分力为

qEcosθ=6.28×10^-7N

粒子受磁场力为f=qv1B=3.94×10-7N

磁场力小于电场力在垂直斜面方向上的分力，粒子没有离开斜面

则第1秒末粒子的速度为62.8m/s．

（2）第2秒内电场力为零，粒子做匀速圆周运动，其周期为T=

2πm

=1s

qv1B=m

mv1

=10m

粒子离开斜面的最大距离L=2r=20m

（3）设粒子离开斜面的速度为v₂

qv₂B=qEcosθ

v₂=100m/s

在斜面上运动的时间t=

mv2

qEsinθ

=1.59s

说明粒子在第3秒内离开斜面

答：（1）第1秒末粒子的速度大小为62.8m/s；

（2）第2秒内粒子离开斜边AD的最大距离20m；

（3）第3秒内粒子能离开斜劈；离开时的速度为100m/s．