如图所示，在倾角为30°的斜面OA的左侧有一竖直档板，其上有一小

问题问答题

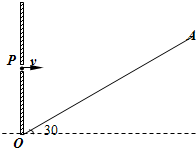
如图所示，在倾角为30°的斜面OA的左侧有一竖直档板，其上有一小孔P，OP=0.5m．现有一质量m=4×10^-20kg，带电量q=+2×10^-14C的粒子，从小孔以速度v₀=3×10⁴m/s水平射向磁感应强度B=0.2T、方向垂直纸面向外的一圆形磁场区域．且在飞出磁场区域后能垂直打在OA面上，粒子重力不计．

求：

（1）粒子在磁场中做圆周运动的半径；

（2）粒子在磁场中运动的时间；

（3）圆形磁场区域的最小半径．

答案

（1）粒子在磁场中，由洛伦兹力提供向心力，根据牛顿第二定律得

qvB=m

得，轨迹半径为 r=

mv0

=0.3m，周期为 T=

2πr

2πm

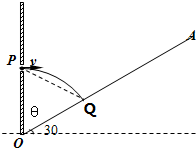
（2）画出粒子运动的轨迹如图，由几何知识得到轨迹对应的圆心角θ=60°，则粒子在磁场中运动的时间为

2π

πm

3qB

×10-5s

（3）当粒子的轨迹圆正好以PQ为直径时，圆形磁场区域的半径最小，根据几何知识得知，PQ=r，则磁场最小的半径为R_min=

=0.15m

答：

（1）粒子在磁场中做圆周运动的半径为0.3m；

（2）粒子在磁场中运动的时间是

×10-5s；

（3）圆形磁场区域的最小半径是0.15m．