已知条件p:x2-3x-4≤0;条件q:x2-6x+9-m2≤0,若p是q的充分不必要条件,则m的取值范围是( )
A.[-1,1]
B.[-4,4]
C.(-∞,-1]∪[1,+∞)
D.(-∞,-4]∪[4,+∞)
由x2-3x-4≤0解得-1≤x≤4,
由x2-6x+9-m2≤0,可得[x-(3+m)][x-(3-m)]≤0,①
当m=0时,①式的解集为{x|x=3};
当m<0时,①式的解集为{x|3+m≤x≤3-m};
当m>0时,①式的解集为{x|3-m≤x≤3+m};
若p是q的充分不必要条件,则集合{x|-1≤x≤4}是①式解集的真子集.
可得
或m<0 3+m≤-1 3-m≥4
,解得m≤-4,或m≥4.m<0 3-m≤-1 3+m≥4
经验证,当m=-4或m=4时,①式的解集均为{x|-1≤x≤7},符合题意.
故m的取值范围是(-∞,-4]∪[4,+∞).
故选D


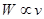 B.
B. 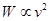 C.
C. 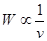 D.
D.