搜题请搜索小程序“爱下问搜题”
问题 问答题

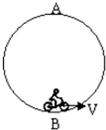
一杂技运动员骑摩托车沿一竖直圆形轨道做特技表演，若车运动的速率恒为20m/s，人与车的总质量为200kg，轮胎与轨道间的摩擦力大小总与它们间的正压力成正比，且比例系数为μ=0.1，车通过最底点B时发动机功率为12kw．

求：（1）车通过最低点B时对轨道的压力？

（2）求车通过最高点A时发动机的功率？

答案

（1）在B点，设发动机功率为PB，则 PB=μFBV，

解得车受到的支持力为 FB=6000N，

 由牛顿第三定律可知，车通过最低点B时对轨道的压力 FB=6000N．    

（2）A、B点人车整体所需向心力大小相等，即m

V2
R
=FB-mg=4000N  

在A点，FA+mg=m

V2
R
，

解得车通过最高点A时对轨道的压力 FA=m

V2
R
-mg=2000N，

则车通过最高点A时发动机的功率 PA=μFAv=4000w=4kw．  

答：（1）车通过最低点B时对轨道的压力是6000N．

（2）车通过最高点A时发动机的功率是4kw．

单项选择题

不属于病人和工作人员辐射防护内容的是()

A、定期对治疗机机头防护的检查 

B、定期对治疗机准直器的防护检查 

C、对建筑屏蔽防护效能的检查 

D、定期对工作人员的剂量防护的检测 

E、对自然本底的剂量检测
查看答案
单项选择题

The Bible is the great work of the religious literature and was in process of formation for about twelve hundred years.

The Bible is composed of (1) , legend, biography, genealogies, ethics, law, proverbial wisdom, sermons, prophesy, lyric poetry, hymns and theology. It is not only (2) a book but a (3) of books.

The Bible (4) two major (5) , the Old Testament and the NewTestament. The Old Testament was written originally almost entirely (6) Hebrew with a little Aramaic, from the eleventh to the second century BC. It is the national (7) literature of the people of Israel. The New Testament was written in Greek from about 40 AD to 150. It 8 the earliest documents (9) the life, teaching, crucifixion and resurrection of Jesus and the establishment of the (10) church. The (11) work is from the first book Genesis, to the last,Revelations.

The (12) and richness of the Bible (13) literature (14) the Old Testament are unparalleled. In the literary (15) , poetry, The Bible is 16 .

The Bible is an assemblage of literature. It is in a unique (17) among the world’s books (18) the richness of its (19) and spiritual values. It can be called the (20) of books.

14（）

A.traditionally

B.conversely

C.especially

D.practically
查看答案