问题
问答题
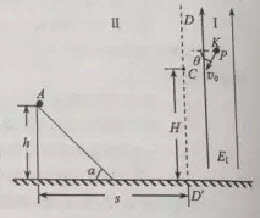
如图所示，图面内有竖直线DD＇，过DD＇且垂直于图面的平面将空间分成Ⅰ、Ⅱ两区域。区域I有方向竖直向上的匀强电场和方向垂直图面的匀强磁场B（图中未画出）；区域Ⅱ有固定在水平面上高h=2l、倾角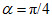
的光滑绝缘斜面，斜面顶端与直线DD＇距离s=4l，区域Ⅱ可知竖直方向的大小不同的匀强电场（图中未画出）；C点在DD＇上，距地面高H=3l。零时刻，质量为m、带电荷量为q的小球P在K点具有大小
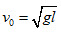、方向与水平面夹角
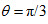的速度，在区域Ⅰ内做半径r=3l/π的匀速圆周运动，经C点水平进入区域Ⅱ。某时刻，不带电的绝缘小球A由斜面顶端静止释放，在某处与刚运动到下颚面的小球P相遇。小球视为质点，不计空气阻力及小球P所带电量对空间电磁场的影响。l已知，g为重力加速度。
（1）求匀强磁场的磁感应强度的大小；
（2）若小球A、P在斜面底端相遇，求释放小球A的时刻tA；
（3）若小球A、P在时刻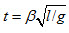
（β为常数）相遇于斜面某处，求此情况下区域Ⅱ的匀强电场的场强E，并讨论场强E的极大值和极小值及相应的方向。
答案
参考答案：
（1）
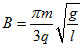；（2）
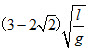（3）场强极小值为
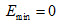；场强极大值为
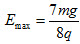，方向竖直向上。
解析：
（1）由题知，小球P在区域Ⅰ内做匀速圆周运动，有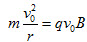
①
代入数据解得
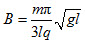②
（3）设所求电场方向向下，在t’A时刻释放小球A，小球P在区域Ⅱ运动加速度为ap，有
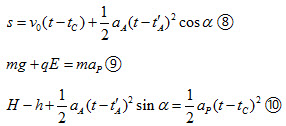
联立相关方程解得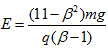
对小球P的所有运动情形讨论可得
由此可得场强极小值为E<sub>min</sub>=0；场强极大值为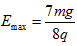
，方向竖直向上。
考点：平抛运动；圆周运动；牛顿第二定律的应用
