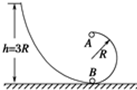
半径为R的光滑半圆环形轨道固定在竖直平面内,从与半圆环相吻合的光滑斜轨上高h=3R处,先后释放A、B两小球,A球的质量为2m,B球的质量为m,当A球运动到圆环最高点时,B球恰好运动到圆环最低点,如图所示.求:
(1)此时A、B球的速度大小vA、vB;
(2)这时A、B两球对圆环作用力的合力大小和方向.
(1)对A分析:从斜轨最高点到半圆环形轨道最高点,由机械能守恒得:
2mg(3R-2R)=
•2m1 2 v 2A
解得:vA=
.2gR
对B分析:从斜轨最高点到半圆环形轨道最低点,由机械能守恒有:
3mgR=
m1 2 v 2B
解得:vB=
.6gR
(2)设半圆环形轨道对A、B的作用力分别为FNA、FNB,FNA方向竖直向下,FNB方向竖直向上.
根据牛顿第二定律得:
FNA+2mg=2m
,FNB-mg=mv 2A R v 2B R
解得:FNA=2mg,FNB=7mg.
根据牛顿第三定律,A、B两球对圆环的力分别为:FNA′=2mg,方向竖直向上;FNB′=7mg,方向竖直向下,所以A、B两球对圆环作用力的合力大小F=5mg,方向竖直向下.
答:
(1)此时A、B球的速度大小分别为
和2gR
.6gR
(2)这时A、B两球对圆环作用力的合力大小5mg,方向竖直向下.
