问题
问答题
如图，在三棱台ABC-DEF中，已知平面BCFE⊥平面ABC，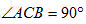
BE=EF=EC=1，BC=2，AC=3，-C
（Ⅰ）求证：BF⊥平面ACFD
（Ⅱ）求二面角B-AD-C的余弦值.
答案
参考答案：
本题主要考查空间点、线、面位置关系，二面角等基础知识，同时考查空间想象能力和运算求解能力。满分15分。
（I）延长AD，BE，CF相交于一点K，如图所示.
因为平面BCFE⊥平面ABC，且AC⊥BC，所以，AC⊥
平面BCK，因此，BF⊥AC.
又因为EF//BC，BE=EF=FC=1，BC=2，所以
ΔBCK为等边三角形，且F为CK的中点，则BF⊥CK.
所以BF⊥平面ACFD.
