如图(a)所示,一质量为m的滑块(可视为质点)沿某斜面顶端A由静止滑下,已知滑块与斜面间的动摩擦因数μ和滑块到斜面顶端的距离x的关系如图(b)所示.斜面倾角为37°,长为L,有一半径为R=
L的光滑竖直半圆轨道刚好与斜面底端B相接,且直径BC与水平面垂直,假设滑块经过B点时没有能量损失.求:1 20
(1)滑块滑至斜面中点时的加速度大小;
(2)滑块滑至斜面底端时的速度大小;
(3)试分析滑块能否滑至光滑竖直半圆轨道的最高点C.如能,请求出在最高点时滑块对轨道的压力;如不能,请说明理由.
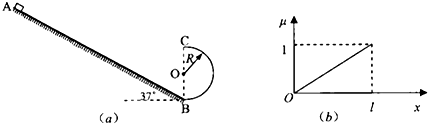
(1)滑块滑到中点时,由(b)图可知,μ=0.5.
根据牛顿第二定律得,mgsin37°-μmgcos37°=ma
解得a=0.2g.
(2)滑块由顶端滑至底端,由动能定理得:mglsin37°+Wf=
mvB21 2
由图b的物理意义得:Wf=
l=-. f
l=-0+mgcos37° 2
mgl2 5
解得:vB=
.
gl2 5
(3)设滑块能运动到C点,则从B到C,由动能定理:-mg•2R=
mvC2-1 2
mvB21 2
解得:vC=
.
gl1 5
如滑块恰好滑到C点:mg=mvC′2 R
解得:vC′=
=gR
<vC
gl1 20
所以滑块能够到达C点
当滑块滑到C点时:mg+N=mvC2 R
解得N=3mg
由牛顿第三定律得滑块在C点时对轨道的压力N′=N=3mg.
答:(1)滑块滑至斜面中点时的加速度大小为0.2g.
(2)滑块滑至斜面底端时的速度大小vB=
.
gl2 5
(3)能滑动半圆轨道的最高点,在最高点时滑块对轨道的压力为3mg.
