问题
问答题
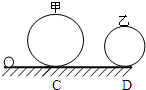
如图所示，半径分别为R和r的甲、乙两个光滑的圆形轨道安置在同一竖直平面上，轨道之间有一条水平轨道CD相通，一质量为m小球以一定的速度先滑上甲轨道，通过动摩擦因数为μ的CD段，又滑上乙轨道，最后离开两圆轨道，若小球在两圆轨道的最高点对轨道的压力都恰好为零，试求：
（1）进入甲轨道最低点C对轨道的压力；
（2）CD段的长度．
答案
（1）在甲轨道最高点，
由牛顿第二定律得：mg=m
，v 21 R
从C点到最高点过程中，
由动能定理得：-2mgR=
mv12-1 2
mvC2，1 2
在C点由牛顿第二定律得：FC-mg=m
，v 2C R
解得：vC=
，FC=6mg，5gR
由牛顿第三定律得，小球在C点对轨道的压力FC′=FC=6mg；
（2）小球在乙最高点，
由牛顿第二定律得：mg=m
，v 22 r
从D到最高点过程中，由动能定理得：
-2mgr=
mv22-1 2
mvD2，解得：vD=1 2
；5gr
从C到D过程中，由动能定理得：
-μmgsCD=
mvD2-1 2
mvC2，1 2
解得：sCD=
；5(R-r) 2μ
答：（1）进入甲轨道最低点C对轨道的压力为6mg；
（2）CD段的长度为
．5(R-r) 2μ
thin → ________________
boy → ________________
long → ________________
teacher → ________________
short → ________________